Réseau de neurones fully connected et convolutionnel
Fully-connected (FC)
Reprenons notre perceptron des sections précédentes :
 Nous notons les entrées $x = [x_1,x_2,x_3,x_4]$ et les poids du perceptron $\omega = [w_1,w_2,w_3,w_4]$. Le résultat du perceptron s'obtient par l'opération matricielle $x \cdot \omega^T$. A cela s'ajoute une non-linéarité (ou fonction d' activation) $f$, la sortie $o = f(x \cdot \omega^T)$. Prenons maintenant un réseau à une couche cachée :
Nous notons les entrées $x = [x_1,x_2,x_3,x_4]$ et les poids du perceptron $\omega = [w_1,w_2,w_3,w_4]$. Le résultat du perceptron s'obtient par l'opération matricielle $x \cdot \omega^T$. A cela s'ajoute une non-linéarité (ou fonction d' activation) $f$, la sortie $o = f(x \cdot \omega^T)$. Prenons maintenant un réseau à une couche cachée :

A la couche cachée 1, nous avons trois sorties $o = [o_1^1,o_2^1,o_3^1]$ où $o_i^j$ est la sortie du perceptron $i$ à la couche $j$. Il y a une matrice de poids $\omega^j$ pour chaque couche cachée $j$ qui assure le mapping de la couche $j-1$ à la couche $j$. Ici, la matrice comprend trois vecteurs de poids, un pour chaque perceptron, qu'on peut écrire comme la matrice $ \omega^1 = \begin{bmatrix}
w_{10} & w_{11} \\
w_{20} & w_{21} \\
w_{30} & w_{31} \\
\end{bmatrix}$ où chaque ligne représente les poids d'un perceptron. La matrice $\omega^j$ est donc taille $|j| \times |j-1| $ où $|j|$ est la taille de la couche $j$. En effet, ici $ \omega^1$ est de taille $3 \times 2 $
On peut écrire la transition complète de la couche $1$ à la couche $2$ comme suit:
$o_1^1 = f(w_{10}^1 x_1 + w_{11}^1 x_2)$
$o_2^1 = f(w_{20}^1 x_1 + w_{21}^1 x_2)$
$o_3^1 = f(w_{30}^1 x_1 + w_{31}^1 x_2)$
$= o^1 = f(x \cdot \omega^{1^T})$
Exercice : Ecrivez l'équation du perceptron de sortie $o_1^2$ (rouge sur le dessin) qui prend en entrées les $o_{\{1..3\}}^1$ de la couche cachée 1. Pour vous aider, écrivez la matrice de poids $\omega^2$.
Il ne faut pas oublier qu'il y a un biais facultatif qui peut s'ajouter par perceptron, auquel cas la matrice $\omega^j$ sera de taille $|j| \times |j-1|+1 $ pour inclure le biais.
Les réseaux fully-connected (FC) ne marchent pas comme on le souhaiterait pour tous types d'entrées. Pour les images, par exemple, des entrées 3 dimensions (hauteur x largeur x RGB), les FC ont des difficultés à converger vers un minimum acceptable. Reprenons le dataset LFW de la précédente section. Les images sont de taille $62\times47\times1$ (greyscale), on devrait donc les aplatir pour en créer des entrées $x \in \mathbb{R}^{2914}$ :
Nombre de classes: (8,)
['Ariel Sharon' 'Colin Powell' 'Donald Rumsfeld' 'George W Bush'
'Gerhard Schroeder' 'Hugo Chavez' 'Junichiro Koizumi' 'Tony Blair']
Dataset shape (1348, 62, 47)
Iter 100 - loss: 1.70
Iter 200 - loss: 1.78
Iter 300 - loss: 1.86
Iter 400 - loss: 1.80
Iter 500 - loss: 1.85
Iter 600 - loss: 1.80
Iter 700 - loss: 1.78
Iter 800 - loss: 1.74
Iter 900 - loss: 1.74
Iter 1000 - loss: 1.85
Iter 1100 - loss: 1.77
Iter 1200 - loss: 1.89
Iter 1300 - loss: 1.69
Iter 1400 - loss: 1.94
Iter 1500 - loss: 1.75
Iter 1600 - loss: 1.77
Iter 1700 - loss: 1.66
Iter 1800 - loss: 1.75
Iter 1900 - loss: 1.75
Nous voyons que le réseau n'arrive pas à converger ni à généraliser les concepts qui pourraient lui permettre de résoudre la tâche.
Réseaux convolutionnels (CNN)
Nous avons majoritairement travailler avec des entrées vectorielles, pour lesquelles les réseaux FC sont parfaitement adaptés. Pour les images, donc des entrées en trois dimensions, nous avons utilisé des convolutions. Rappelez-vous du réseau que l'on a utilisé :
Nous pouvons voir que le réseau est composé d'une succession de couches de convolutions et de pooling. Dans les sections suivantes, nous décrivons à quoi elles correspondent :
Convolutions
Définition : En analyse fonctionnelle, la convolution est une opération mathématique sur deux fonctions $f$ et $g$ qui produisent une troisième fonction qui exprime comment les formes de ces deux fonctions interagissent entre elles. Une convolution est définie par l'intégrale suivante :
$$(f * g)(t) \triangleq\ \int_{-\infty}^\infty f(\tau) g(t - \tau) \, d\tau$$
qui se traduit par un "glissement" de valeur $\tau$ de la fonction $g$ sur la fonction $f$ :

Nous allons voir comment ce concept se traduit dans le domaine des réseaux de neurones. Premièrement, le neurone, appelé dans le cas des Réseaux de neurones convolutifs (Convolutional Neural Networks, CNN) filtre ou champ réceptif, est représenté par $g$. C'est donc lui qui va glisser sur une entrée $f$ représentée soit par les entrées $x$ ou par la sortie d'une précédente couche de convolution. Considérons l'image suivante :
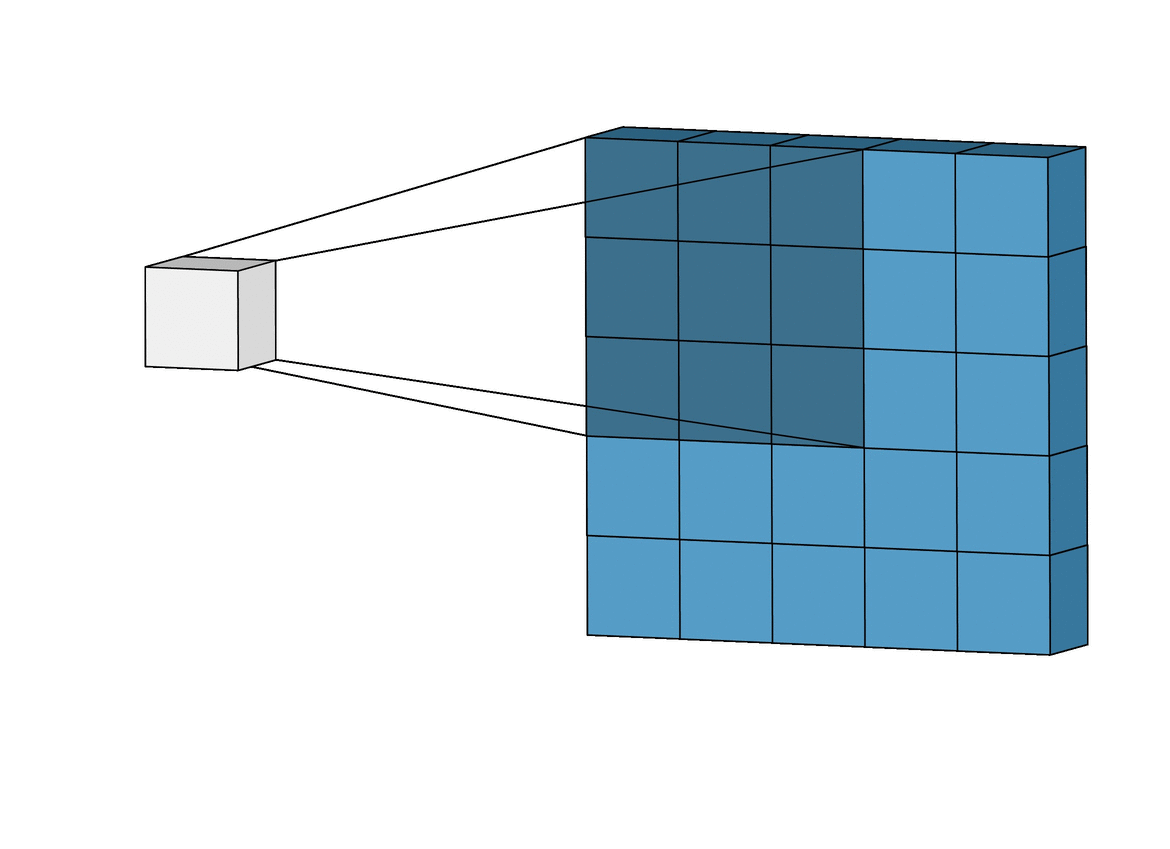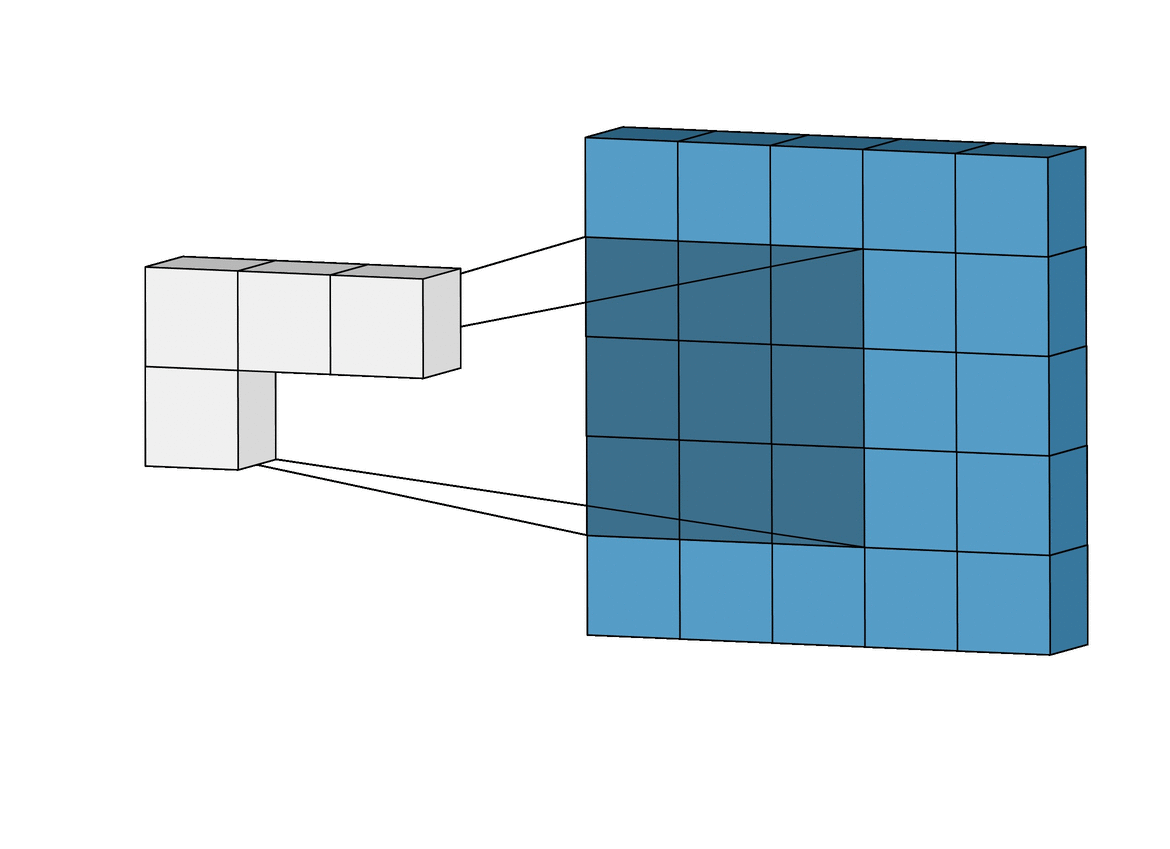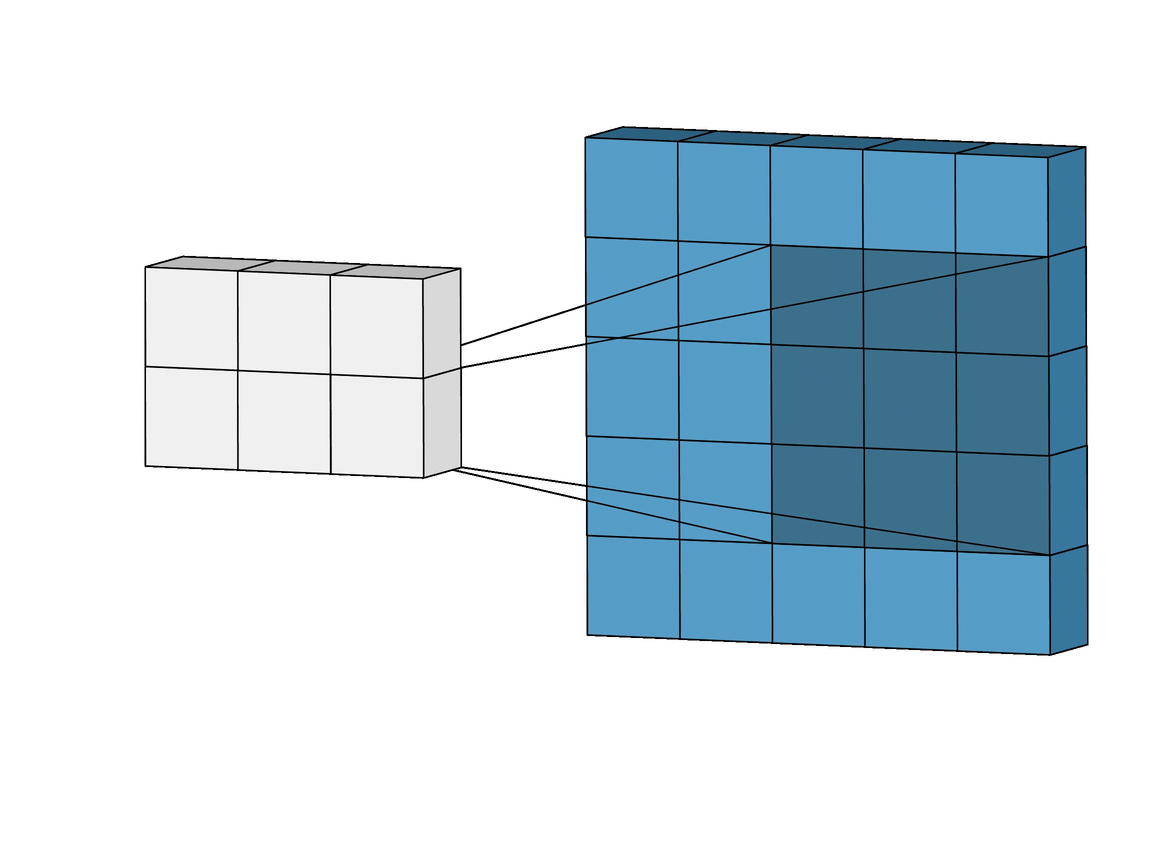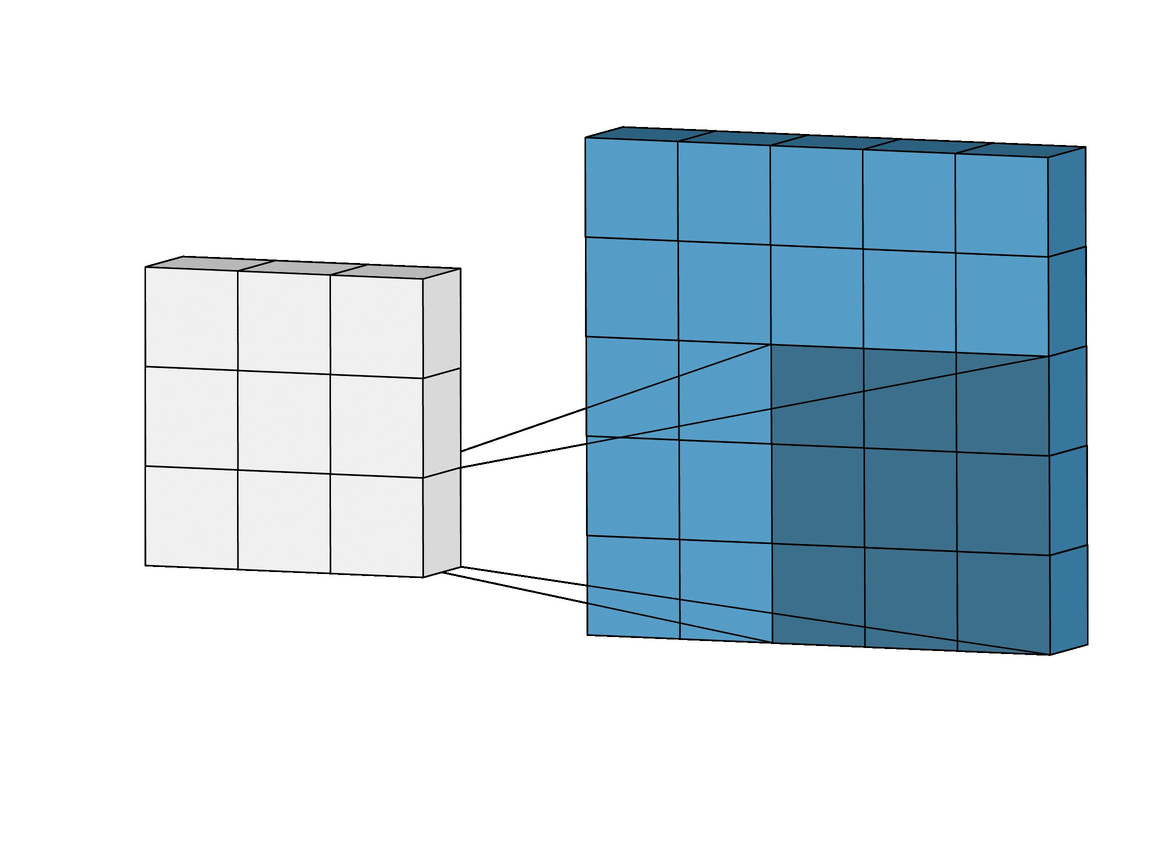 Nous y trouvons :
Nous y trouvons :
- des entrées deux dimensions, en bleu clair (ou $f$)
- le neurone (perceptron) ou le filtre ($g$), en bleu foncé, qui glisse (convolve en anglais) sur les entrées bleues claires
- le résultat qui se construit au fur et à mesure de la convolution, en gris $(f * g)$
Sur cet exemple, le filtre est de dimension $3\times3\times1$ et comprend donc 9 poids (10 si biais facultatif désiré). La sortie d'un glissement est la somme du produit matriciel de Hadamard de la matrice de poids du filtre et de l'input à l'endroit où se trouve le filtre.
Imaginons que le perceptron a pour matrice de poids (on omet le biais) $ \omega = \begin{bmatrix}
1 & 0 & 1 \\
0 & 1 & 0 \\
1 & 0 & 1 \\
\end{bmatrix}$, voici le résultat du premier glissement :

Définition : Soit A la matrice des poids du filtre et B la matrice de l'input à l'endroit du filtre et $C$ le résultat, la convolution pour des entrées discrètes à deux dimensions s'écrit :
$$C \left[ m, n \right] = \sum_u \sum_υ A \left[ m + u, n + υ\right] \cdot B \left[ u, υ \right]$$
Nous voyons que chaque élément de $C$ est calculé comme la somme des produits de chaque élément de A et B.
En effet, on voit que chaque glissement produit uniquement un carré gris. La convolution réalise 9 glissements au total, nous avons donc une sortie de $9 \times 1 $ ou de $3 \times 3 \times 1$.
Une couche convolutive est nuancée par trois paramètres :
- Sa profondeur (depth) : qui correspond au nombre de filtres (de cellules) qui vont glisser sur le même input. Dans le cas précédent, si on ajoutait un deuxième filtre, la sortie grise serait de taille $3 \times 3 \times2$.
- Son pas (stride): qui correspond au "saut" que fait le filtre à chaque glissement. Dans l'exemple précédent, le saut est de 1.
- Zero-padding : qui correpond à l'ajout d'un bord de 0 (autour de l'input) pour privilégier une taille de sortie que l'on préfèrerait. Le filtre passe sur ces 0 et donc augmente son volume de sorties.
On peut définir la formule de taille de sorties en fonction de l'entrée assez facilement. Soit une entrée de taille $W$, un filtre de taille $F$, un stride $S$ et un nombre de bords zero-padding $P$, la sortie est donnée par : $(W - F + 2P)/S + 1$. Pour l'exemple précédent, nous obtenons $(5 - 3 + 0)/1 + 1 = 3$. Donc notre output est bien de $3 \times 3 \times 1 $.
Exercice : Appliquez la formule pour le problème suivant et vérifiez votre solution. Le bord blanc est un zero-padding :
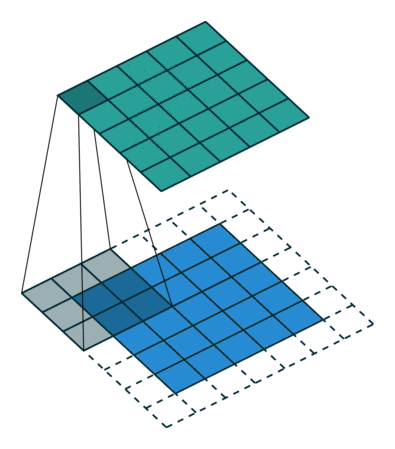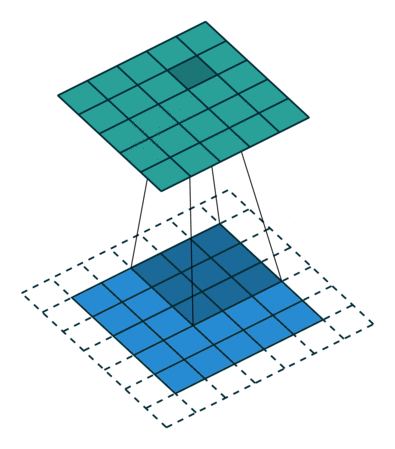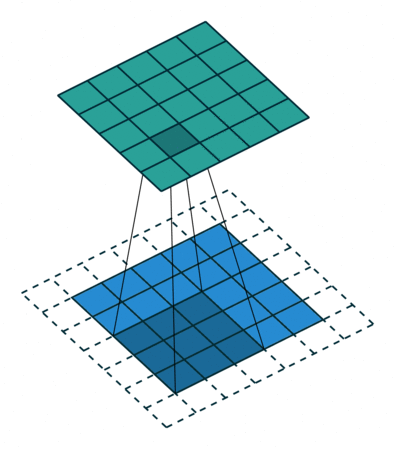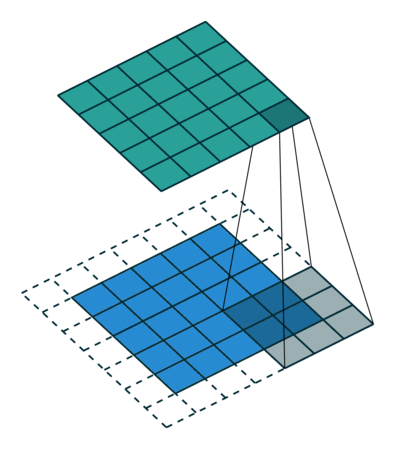
Imaginez le même exercice mais avec un stride $S$ de 3 : cette convolution est-elle possible ?
A l'inverse du perceptron fully-connected, le perceptron convolutionnel (le filtre) n'a qu'une connectivité locale en espace. Nous pouvons vérifier cela avec notre schéma de perceptrons :
 Le résultat d'un glissement ne prend que 3 entrées vertes pour un résultat bleu, et non plus toutes les entrées comme le fully-connected. Notons aussi comme différence que le perceptron convolutionelle génère plusieurs sorties. La connectivité locale est encore plus évidente si on augmente le stride $S$ :
Le résultat d'un glissement ne prend que 3 entrées vertes pour un résultat bleu, et non plus toutes les entrées comme le fully-connected. Notons aussi comme différence que le perceptron convolutionelle génère plusieurs sorties. La connectivité locale est encore plus évidente si on augmente le stride $S$ :

Attention : Si la connectivité est locale en espace, la connectivité est
pleine dans la profondeur. Si une entrée est de taille $W \times W \times 3$ (une image RGB, par exemple), le filtre sera de taille $F \times F \times 3$, comme nous le voyons sur l'image suivante :
 Cependant, la taille de la sortie sera toujours le même
Cependant, la taille de la sortie sera toujours le même : le filtre produit toujours une sortie par glissement, peu importe la profondeur. Il y a juste plus de multiplications et de sommes pour obtenir le résultat.
Enfin, une couche de convolution peut comprendre plusieurs filtres. Sa sortie est donc l'empilement des résultats pour chaque filtre. Reprenons le premier exemple de cette section : l'image était de taille $5 \times 5 \times 1$, le filtre de taille $3 \times 3 \times 1$ et le résultat du filtre $3 \times 3 \times 1$. Si l'on décide pour cette couche de convolution d'avoir 15 filtres (avec chacun son propre ensemble de poids), la sortie de la couche de convolution est de $3 \times 3 \times 15$.
Exercice : Comprendre le résultat de cette couche de convolution à 2 filtres pour une entrée de profondeur $3$ :
Crédit de l'animation : Stanford University
Grâce à l'entrainement, chaque filtre va se spécialiser dans la reconnaissance d'une caractéristique (ou feature) que l'on pourrait trouver dans une image : une forme, une couleur, un bord, un pattern, ... Un instigateur des convolutions pour réseaux de neurones, Alex Krizhevsky, propose son réseau CNN AlexNet en 2012 qui révolutionnera le champ de vision par ordinateur. Dans le rapport scientifique, les auteurs donnent une intuition sur ce que les filtres de taille $11 \times 11 \times 3$ à la première couche de convolution ont appris en les interprètant en image RGB :

Pooling
Entre chaque couche de convolution, nous introduisons une couche de "pooling" sur les dimensions spatiales des cartes de features (les sorties de chaque filtre empilées ensemble). La technique la plus utilisée s'appelle le max-pooling et consiste à garder la feature la plus dominante parmi son voisinage. Voici un exemple pour un max-pooling de 2, stride 2 :
 Nous remarquons que la profondeur, ici de dimension 64, reste inchangée.
Nous remarquons que la profondeur, ici de dimension 64, reste inchangée.
Il convient de réaliser un "pooling" pour deux raisons :
- Réduction de dimension : Réduire la dimension de l'entrée et donc les coûts computationels
- Invariance positionnelle : Extraire les features les plus importantes dans la région peu importe sa position dans le voisinage
Avec ces deux concepts, le pooling et les convolutions, nous pouvons former un CNN de la façon suivante :



